Simple steps to calculate sample clock jitter for an isolated precision high-speed DAQ

“Jitter in the signal (or clock) that controls the sample-and-hold switches in the ADC can affect the SNR performance of a precision high-speed DAQ signal chain. When selecting the various components that make up a clock signal chain, it is important to understand the various error sources that add to the overall jitter.

“

By Lloben Paculanan, Application Development Engineer, Analog Devices
John Neeko Garlitos, Product Applications Engineer, Analog Devices

Introduction

Many data acquisition (DAQ) applications require isolation of the DAQ signal chain path for reasons of robustness, safety, high common-mode voltage, or to eliminate ground loops that can introduce errors in measurements. ADI’s precision high-speed technology enables system designers to achieve high AC and DC accuracy in the same design without sacrificing DC accuracy for higher sampling rates. However, to achieve high ac performance, such as signal-to-noise ratio (SNR), system designers must account for errors introduced by jitter on the sampling clock signal or the conversion start signal that controls the sample-and-hold (S&H) switches in the ADC. As the target signal and sample rate increase, the signal jitter controlling the sample-and-hold switch can become a major source of error.

When the DAQ signal chain is isolated, the signal that controls the sample-and-hold switch typically comes from the backplane that performs simultaneous multi-channel sampling. It is critical for the system designer to select a low-jitter digital isolator so that the control signal entering the ADC’s sample-and-hold switch has low jitter. Precision high-speed ADCs should preferably use the LVDS interface format to meet high data rate requirements. It also causes minimal disturbance to the DAQ power and ground planes. This article will explain how to interpret the jitter specifications of ADI’s LVDS digital isolators and how they compare with precision high-speed products such as the ADAQ23875DAQ µModule^®solution), which specifications are more important. These guidelines in this article also apply to other precision high-speed ADCs with LVDS interfaces. When introducing the ADAQ23875 used with the ADN4654 Gigabit LVDS isolator, the methodology used to calculate the expected impact on SNR will also be described.

How Jitter Affects the Sampling Process

Typically, clock sources have jitter in the time domain. When designing a DAQ system, it is important to know how much jitter is included in the clock source.

Figure 1 shows a typical output spectrum of a non-ideal oscillator with noise power as a function of frequency in a 1 Hz bandwidth. Phase noise is defined as a specified frequency offset f_mNoise vs fundamental frequency f in the lower 1 Hz bandwidth_oThe ratio of the lower oscillator signal amplitude.

Figure 1. Oscillator Power Spectrum Affected by Phase Noise

The sampling process is the multiplication of the sampling clock by the analog input signal. This multiplication in the time domain is equivalent to convolution in the frequency domain. Therefore, during ADC conversion, the spectrum of the ADC sampling clock is convolved with the pure sine wave input signal, so that jitter on the sampling clock or phase noise appears in the FFT spectrum of the ADC output data, as shown in Figure 2.

Figure 2. Effect of a sampling clock with phase noise on sampling an ideal sine wave

Isolated Precision High Speed ​​DAQ Applications

A multiphase power analyzer is an example of an isolated precision high-speed DAQ application. Figure 3 shows a typical system architecture where channel-to-channel isolation is used to communicate with system computing or controller modules through a shared backplane. In this example, we chose the ADAQ23875 precision high-speed DAQ solution because its small size allows for easy installation of multiple isolated DAQ channels in tight spaces, which can reduce the weight of mobile instruments in field test applications. The DAQ channel is isolated from the main chassis backplane using an LVDS Gigabit isolator (ADN4654).

By isolating each DAQ channel, each channel can be directly connected to sensors with different common-mode voltages without damaging the input circuitry. The ground of each isolated DAQ channel tracks the common-mode voltage with some voltage offset. If the DAQ signal chain can track the common-mode voltage associated with the sensor, there is no need to use input signal conditioning circuits to support larger input common-mode voltages and eliminate the higher common-mode voltages for downstream circuits. This isolation also provides safety and eliminates ground loops that can affect measurement accuracy.

In power analyzer applications, it is critical to achieve synchronization of sampling events across all DAQ channels, as the mismatch of time domain information related to the sampled voltage can affect subsequent calculations and analysis. To synchronize sampling events between channels, the ADC sampling clock is sent from the backplane through LVDS isolators.

In the isolated DAQ architecture shown in Figure 3, these following sources of jitter error add to the overall jitter on the sampling clock that controls the sample-and-hold switches in the ADC.

1. Reference clock jitter

The first source of sample clock jitter is the reference clock. This reference clock is transmitted through the backplane to each isolated precision high-speed DAQ module and other measurement modules that plug into the backplane. This clock is used as a timing reference for the FPGA; therefore, the timing accuracy of all events, digital blocks, PLLs, etc. in the FPGA depends on the accuracy of the reference clock. In some applications without a backplane, the onboard clock oscillator is used as the reference clock source.

2. FPGA jitter

The second source of sampling clock jitter is the jitter introduced by the FPGA. Note that a trigger-to-execute path is included in the FPGA, and the jitter specifications of the PLL and other data blocks in the FPGA can affect the overall jitter performance of the system.

3. LVDS isolator jitter

A third source of sampling clock jitter is the LVDS isolator. LVDS isolators generate additional phase jitter that affects the overall jitter performance of the system.

4. Aperture jitter of ADC

A fourth source of sampling clock jitter is the ADC’s aperture jitter. This is an inherent characteristic of the ADC itself, please refer to the data sheet for a specific definition.

Figure 3. Isolated DAQ architecture from channel to channel

Some reference clock and FPGA jitter specifications are given based on phase noise. To calculate the jitter contribution to the sampling clock, the phase noise specification in the frequency domain needs to be converted to a jitter specification in the time domain.

Calculate jitter from phase noise

The phase noise curve is somewhat similar to the input voltage noise spectral density of an amplifier. As with amplifier voltage noise, it is best to use a low 1/f corner frequency in the oscillator. Oscillators often use phase noise to describe performance, but in order to correlate phase noise to ADC performance, phase noise must be converted to jitter. To correlate the graph in Figure 4 to modern ADC applications, an oscillator frequency (sampling frequency) of 100 MHz was chosen for ease of discussion, and a typical curve is shown in Figure 4. Note that the phase noise curve is fitted by multiple line segments, the endpoints of each segment are defined by data points.

Figure 4. Calculating jitter from phase noise

When calculating equivalent rms jitter, the first step is to obtain the integrated phase noise power in the frequency range of interest, area A of the curve. The curve is divided into separate regions (A1, A2, A3, and A4), each defined by two data points. Assuming no filtering between the oscillator and the ADC input, the upper limit of the integration frequency range should be 2 times the sampling frequency, which is approximately the bandwidth of the ADC sampling clock input. The choice of the lower limit of the integral frequency range also needs some consideration. In theory, it should be as low as possible in order to get true rms jitter. In practice, however, manufacturers generally do not give oscillator characteristics for offset frequencies less than 10 Hz, but this can be calculated with sufficient accuracy. In most cases, it is reasonable to choose 100 Hz as the lower limit of the integral frequency if the characteristic at 100 Hz is provided. Otherwise, 1 kHz or 10 kHz data points can be used. It should also be considered that close-in phase noise affects the spectral resolution of the system, while broadband noise affects the overall system signal-to-noise ratio. Perhaps the most sensible approach is to integrate each region separately and examine the magnitude of the jitter contribution of each region. If a crystal oscillator is used, the low frequency contribution may be negligible compared to the broadband contribution. Other types of oscillators may have considerable jitter contributions in the low frequency region, and their importance to the overall system frequency resolution must be determined. The integration of each region yields individual power ratios, which are then summed and converted back to dBc. Once the integrated phase noise power is known, the rms phase jitter (in radians) can be calculated by:

Divide the above result by 2πf₀you can convert a jitter of 0 in radians to a jitter in seconds:

See “MT-008 Tutorial: Converting Oscillator Phase Noise to Time Jitter” for more details.

Quantize reference clock jitter

The reference clock source used in high-performance DAQ systems is typically a crystal oscillator, which provides better jitter performance than other clock sources.

We generally define crystal oscillator jitter specifications in data sheets using the examples shown in Table 1. Phase jitter is the most important specification when quantifying the jitter contribution of a reference clock. Phase jitter is generally defined as the deviation of edge position relative to the average edge position.

Table 1. Examples of crystal oscillator jitter specifications given in the data sheet

On the other hand, there are crystal oscillators that specify phase noise performance, not jitter. If the oscillator data sheet defines phase noise performance, the noise value can be converted to jitter, as described in the “Calculating Jitter from Phase Noise” section.

Quantify jitter from FPGA

The main function of the reference clock in the FPGA is to provide a trigger signal to start different parallel events set in the FPGA. In other words, the reference clock coordinates all events in the FPGA. In order to provide better time resolution, the reference clock is usually passed to the PLL in the FPGA to increase its frequency, therefore, short time interval events may occur. Also, note that the FPGA contains a trigger-to-execute path where the reference clock is passed to clock buffers, counters, logic gates, and so on. When dealing with jitter-sensitive repetitive events (eg, LVDS convert-start signal to ADC through isolation), it is necessary to quantify the jitter contribution from the FPGA to reasonably estimate the impact of overall system jitter on high-speed data acquisition performance.

The jitter performance of an FPGA is usually given in the FPGA data sheet. It is also given in the Static Timing Analysis (STA) of most FPGA software tools, as shown in Figure 5. Timing analysis tools can calculate the clock uncertainty at the source and destination of the datapath and combine them to obtain the total clock uncertainty. In order to automatically calculate the amount of reference clock jitter in STA, it must be added as an input jitter constraint in the FPGA project.

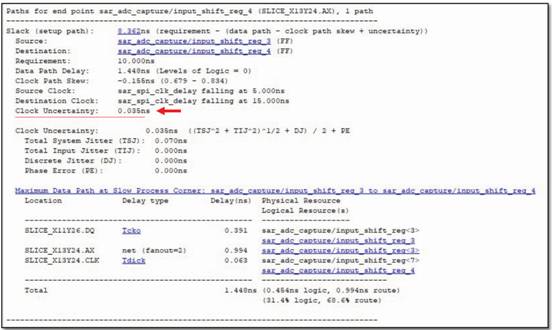
Figure 5. Static Timing Analysis (STA) Example View

Quantifying jitter from digital isolation

The most basic way to view jitter is to measure the LVDS signal pair with a differential probe, trigger on both rising and falling edges, and set the oscilloscope to last infinitely. This means that high-to-low and low-to-high transitions are superimposed on each other, so the crossover point can be measured. The crossover width corresponds to the peak-to-peak jitter or time interval error (TIE) measured to date. Compare the eye diagram and histogram shown in Figure 6 and Figure 7. Some jitter is due to random sources (such as thermal noise), this random jitter (RJ) means that the peak-to-peak jitter seen on the oscilloscope is limited by the run time (as the run time increases, the tails on the histogram will change. rise).

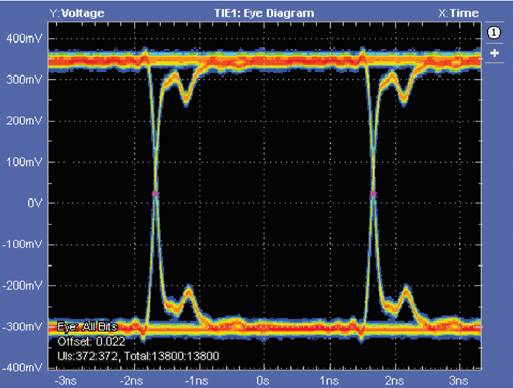
Figure 6. Eye diagram of the ADN4651

Figure 7. Eye Diagram Histogram of ADN4651

In contrast, deterministic jitter (DJ) sources are bounded, such as jitter due to pulse skew, data-dependent jitter (DDJ), and intersymbol interference (ISI). Pulse skew arises from the difference between high-to-low and low-to-high propagation delays. This can be visualized by offset crossing, that is, at 0 V, the two edges are separated (easy to see by the separation within the histogram in Figure 7). DDJ stems from the difference in propagation delay at different operating frequencies, while ISI stems from the effect of the previous transition frequency on the current transition (eg, edge timing usually differs after a series of 1s or 0s versus 1010 pattern codes).

Figure 8. Total Jitter Contribution Sources

Figure 8 shows how to adequately estimate the total jitter (TJ @BER) at a given bit error rate. Random and deterministic jitter can be calculated from the state of the fit between the model and the measured TIE assignments. One such model is the double Dirac model, which assumes a Gaussian random distribution convolved with a double Dirac delta function (the separation distance between two Dirac delta functions corresponds to deterministic jitter). For a TIE distribution with significant deterministic jitter, the distribution visually approximates this model. One difficulty is that some deterministic jitter can affect the Gaussian component, that is, the double Dirac function may underestimate deterministic jitter and overestimate random jitter. However, the combination of the two still provides an accurate estimate of the total jitter at a given bit error rate.

Random jitter is specified as a 1 σ rms value in a Gaussian distribution model, to extrapolate longer run lengths (low BER), simply choose an appropriate polyσ that moves a sufficient distance along the tail of the distribution (e.g. , 1 × 10^-12A bit error requires 14 σ) is enough.Then join the DJ to[email protected]